你见过中考数学中的黄金分割问题吗这道题的答案(中考数学黄金分割典型例题)

导语：你见过中考数学中的黄金分割问题吗？这道题蛮有意思的，解法新颖

这是一道中考数学与黄金分割有关的压轴题，通常在中考数学中很少见到黄金分割的问题，别说压轴题了，就是普通的小题，也是难得一见的。所以这道题特别引起老黄的注意。题目是这样的：

正方形ABCD ，点M为边AB的中点.

(1)如图1, 点G为线段CM上的一点，且∠AGB=90度，延长AG，BG分别与边BC，CD交于点E，F. 求证：①BE=CF；②BE^2=BC·CE.

(2)如图2，在边BC上取一点E，满足BE^2=BC·CE，连接AE交CM于点G，连接BG延长交CD于点F，求tan∠CBF的值.

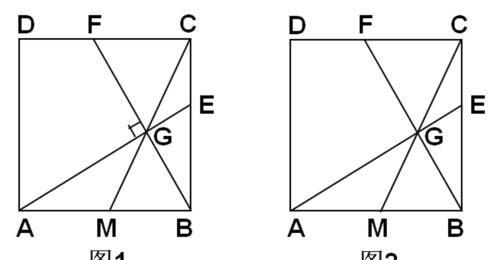
分析：(1)①很明显要通过全等三角形证明对应边相等。观察两条线段所在的三角形，它们分别在直角三角形ABE和直角三角形BEG中，凑一凑全等的条件。在正方形中，有边AB=CB，内角都是直角，所以∠ABE=∠BCF=90度.

在直角三角形ABE和直角三角形BEG中，两组锐角都互余，关键这两组互余的锐角有一个公共角AEB，因此另外两个角相等，即∠BAE=∠CBF，这是等角等余定理的应用。

这就构成了两个三角形“角边角”的全等条件，因此它们的对应边BE=CF。

②显然要利用有公共边的相似三角形的边的关系。然而BE做为公共边的相似三角形是直角三角形ABE和直角三角形BGE，它们是推不出这个关系的。因此BE要转换，转换成CF也解决不了。通过观察，如果能够证明三角形CEG和三角形CGB相似，且CG等于BE，那么就可以得到要证明的结论。

首先，由于M是直角三角形ABG斜边AB的中点，所以中线GM等于斜边的一半，也就等于AM。由等边对等角，就有角GAM等于角AGM。而角AGM等于角CBG，它们是全等三角形的对应角。

所以角CGF等于它的对顶角BGM，而角BGM又等于角CFG，因为它们分别是角AGM和角CBG的余角，即等角等余定理的应用。

根据等角对等边，就有CG=CF。而CF又等于BE，从而CG就等于BE。

另一方面，角CGE和角AGM是对顶角，从而角CGE也等于角CBG。这就构成了相似三角形的“两组内角相等”的条件。由相似三角形的边成比例的关系，就可以推出CG^2=BE^2=BC·CE.

(2)这个角的正切值很好表示出来，就是CF/BC. 很明显的，只要能证明BE等于CF，就可以得到答案。因为点E其实就是BC靠近端点C的黄金分割点，这个比值是可求的。甚至是可以直接写出来的。

将CE=BC-BE代入BE^2=BC·CE，可以得到关于BE的二次方程，运用求根公式，就可以得到BE关于BC的表达式，也就是得到它们的比值。

接下来证明BE=CF，这无疑是第一小题的一个逆过程。然而直接反推，并不能实现，那应该怎么办呢？只要我们能够证明∠AGB=90度，由(1)就可以直接得到BE=CF。

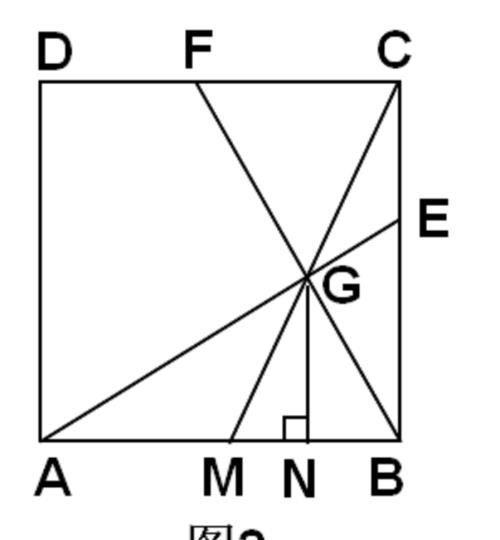
为此，我们过G作AB的垂线段GN，则直角三角形GMN和直角三角形CMB相似。再结合平行线截取线段成比例的关系，可以得到两组线段（边）的比例关系，从而转换出MN，GN关于BC的表达式。再运用勾股定理，就可以得到GM=BC/2，从而证明∠AGB=90度，问题就解决了。下面组织解题过程：

(1)证明：在正方形ABCD中，AB=CB，∠ABE=∠BCF=90度，

在Rt△ABE中，∠BAE+∠AEB=90度，

∵∠AGB=90度，∴在Rt△BEG中，∠CBF+∠AEB=90度，

∴∠BAE=∠CBF，∴Rt△ABE≌Rt△BCF(ASA)，

①∴BE=CF.

②在Rt△ABG中，点M是AB的中点，

∴GM=AB/2=AM, ∴∠GAM=∠AGM=∠CBG,

∴∠CGF=∠BGM=∠CFG(等角等余), ∴ CG=CF=BE，

又∠CGE=∠AGM=∠CBG, ∴△CGE∽△CBG,

∴CG/CB=CE/CG，即CG^2=BE^2=BC·CE.

(2)解：由BE^2=BC·CE, 有BE^2=BC·(BC-BE),

从而BE^2+BC·BE-BC^2=0, 解得：BE=(根号5-1)BC/2(舍去负值),

过G作GN⊥AB于点N, 则Rt△GMN∽Rt△CMB,

GN/MN=CB/MB=AB/MB=2,

又GN/BE=AN/AB, 即4MN/((根号5-1)BC)=(AB/2+MN)/AB=1/2+MN/BC,

解得MN=根号5 BC/10, GN=2倍根号5 BC/10,

MG=根号(MN^2+GN^2)=BC/2=AB/2, ∴∠AGB=90度,由(1)有BE=CF,

∴tan∠CBF=CF/BC=BE/BC=(根号5-1)/2.

第二小题还有另一种解法。这种方法不是很常规，但特别简便，大家可以看看这样解是否合理。它运用的是反证法，初中阶段，也已经学过反证法了。

(2)解：由BE^2=BC·CE知, E点是BC靠近点C的黄金分割点,

若∠AGB≠90⁰, 则由(1)可知，存在E’满足BE’^2=BC·CE’,

即E’点也是BC靠近点C的黄金分割点, 矛盾！

∴∠AGB=90度, 由(1)有BE=CF,∴tan∠CBF=CF/BC=BE/BC=(根号5-1)/2.

你对最后这种解法有什么看法，欢迎在评论区中留下乐的观点。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小洁创作整理编辑！