数学中考拔高题哪个好(中考数学题用高中方法算不算对)
导语:中考数学高分不在于题海战术,而在于思想方法

初三开学已经快一个月,很多学生已经感受到初三学习的难度和综合性,多多少少都会感受到一些中考的压力。
相比初一初二这两年来说,初三的学习内容无论是深度还是广度,都大大加强。同时,初三的学习内容又是基于初一初二这两年所学的知识上,进一步深化和提高。
因此,如果大家进入初三后,发现学习遇到困难多起来,就要学会检查自己的基础知识掌握的是否扎实,知识链上有没有出现“断层”。同时,要学会正确认识到初三学习的复杂性,如会出现大量与函数有关的综合性问题。
函数的学习可以说是贯穿了整个中学数学的学习,一直是中考必考的热门考点。函数的复杂性不仅仅是体现在自身内容复杂性上,贯穿于几何、代数等等各个知识板块当中,蕴含丰富的数学思想,形成更为复杂的综合性问题。
如数形结合思想就是在解决与函数相关问题时候,常常需要用到的数学思想方法。这主要是基于函数本身的特殊性,研究函数,我们首先就需要搞懂函数的图象与性质,学会把函数解析式转化成函数图象,或是把函数图象转化成具体的解析式来解决问题等等,以上这些都是数形结合思想在函数综合问题当中的体现。

在数学学习中,我们会碰到很多数学思想方法,数形结合就是最常用的思想方法之一。所谓数形结合,就是根据数与形之间的对应关系,通过数与形的相互转化来解决数学问题的思想,实现数形结合。
运用数形结合的思想,我们可以使某些抽象的数学问题直观化、生动化,能够变抽象思维为形象思维,有助于把握数学问题的本质,这样很多问题便迎刃而解,且解法容易理解和消化。
数形结合思想常与以下内容有关:
1实数与平面直角坐标系上的点的对应关系;
2函数与图象的对应关系;
3函数与方程的对应关系(如二次函数与一元二次方程等);
4以几何为背景建立起来的数学模型,综合运用代数、函数等知识,此类型题难度较大。
从近几年中考试题的变化,我们不难发现如果能巧妙运用数形结合这一方法,可以很好帮助我们去解决一些综合性数学问题,帮助我们提高数学成绩。
典型例题分析1:
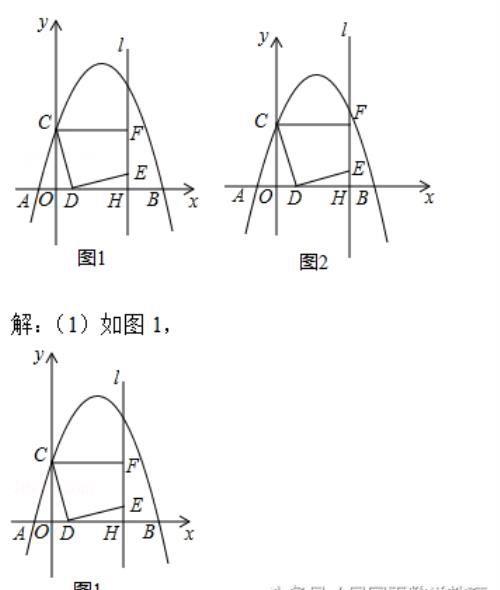
如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
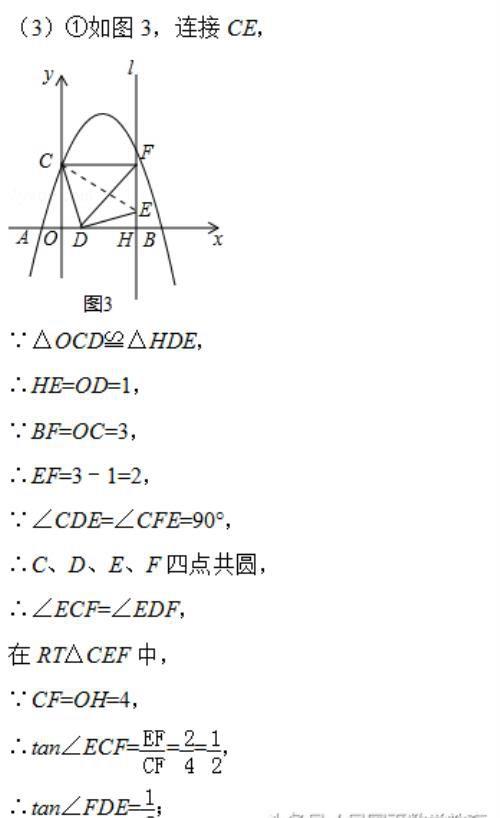
①连接DF,求tan∠FDE的值;
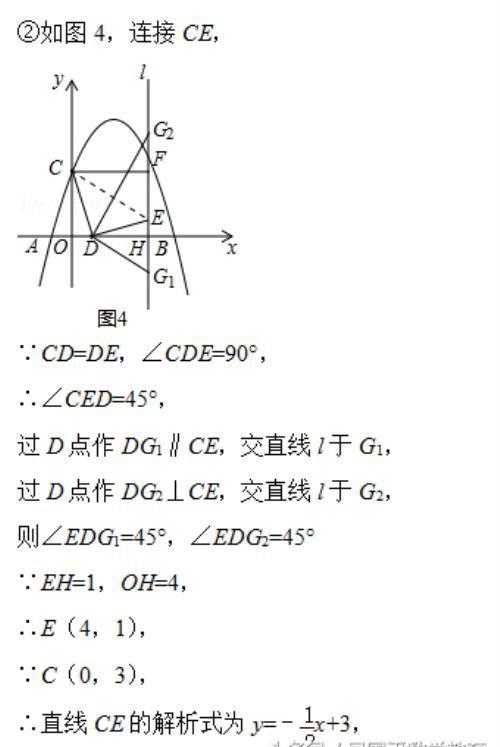
②试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.


考点分析:
二次函数综合题.
题干分析:
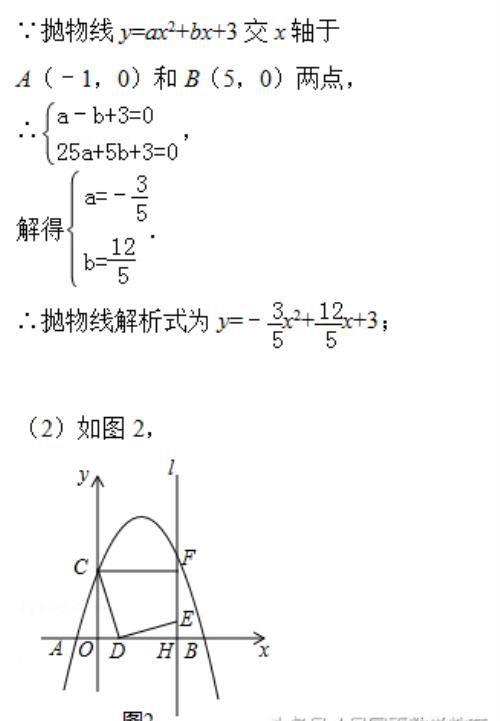
(1)利用待定系数法求得即可;
(2)根据C的纵坐标求得F的坐标,然后通过△OCD≌△HDE,得出DH=OC=3,即可求得OD的长;
(3)①先确定C、D、E、F四点共圆,根据圆周角定理求得∠ECF=∠EDF,由于tan∠ECF=EF/CF=2/4=1/2,即可求得tan∠FDE=1/2;
②连接CE,得出△CDE是等腰直角三角形,得出∠CED=45°,过D点作DG1∥CE,交直线l于G1,过D点作DG2⊥CE,交直线l于G2,则∠EDG1=45°,∠EDG2=45°,求得直线CE的解析式为y=﹣1/2x+3,即可设出直线DG1的解析式为y=﹣1/2x+m,直线DG2的解析式为y=2x+n,把D的坐标代入即可求得m、n,从而求得解析式,进而求得G的坐标.
解题反思:
本题是二次函数的综合题,考查了待定系数法求二次函数的解析式,一次函数的解析式,三角形全等的判定和性质,等腰直角三角形的性质,平行线的性质等,数形结合思想的应用是解题的关键。

数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系,寻求代数问题的解决方法(以形助数),或利用数量关系来研究几何图形的性质,解决几何问题(以数助形)的一种数学思想. 数形结合思想使数量关系和几何图形巧妙地结合起来,使问题得以解决。
数学思想方法是数学的灵魂和精髓,数学思想方法无论在数学专业领域、数学教育范围内,还是在其它科学中,都被广为使用。因此,学好数学思想方法,对于我们学好数学是可以起到很大的帮助。
典型例题2:
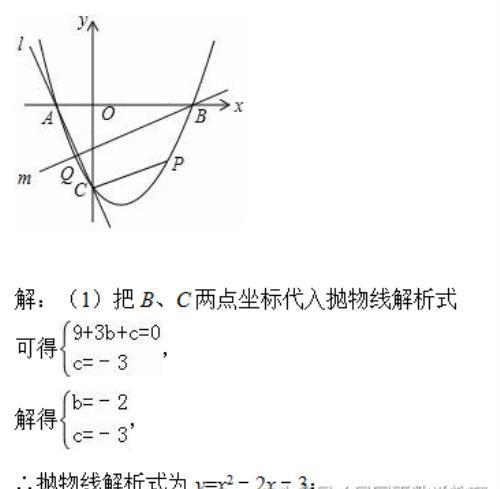
如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由。



考点分析:
二次函数综合题.
题干分析:
(1)由B、C两点的坐标,利用待定系数法可求得抛物线的解析式;
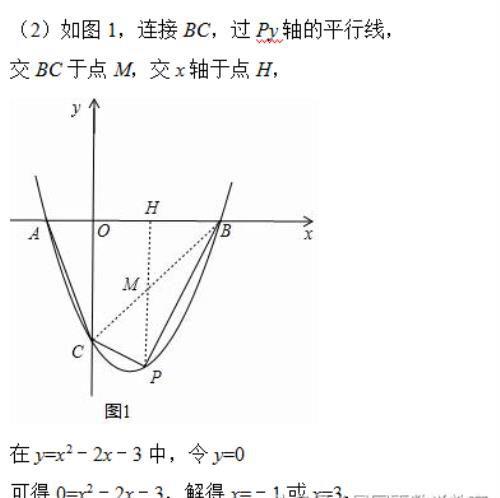
(2)连接BC,则△ABC的面积是不变的,过P作PM∥y轴,交BC于点M,设出P点坐标,可表示出PM的长,可知当PM取最大值时△PBC的面积最大,利用二次函数的性质可求得P点的坐标及四边形ABPC的最大面积;
(3)设直线m与y轴交于点N,交直线l于点G,由于∠AGP=∠GNC+∠GCN,所以当△AGB和△NGC相似时,必有∠AGB=∠CGB=90°,则可证得△AOC≌△NOB,可求得ON的长,可求出N点坐标,利用B、N两的点坐标可求得直线m的解析式.
解题反思:
本题为二次函数的综合应用,涉及知识点有待定系数法、二次函数的最值、相似三角形的判定、全等三角形的判定和性质等。
在(2)中确定出PM的值最时四边形ABPC的面积最大是解题的关键,在(3)中确定出满足条件的直线m的位置是解题的关键。
本题考查知识点较多,综合性较强,特别是第(2)问和第(3)问难度较大。
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小婷创作整理编辑!