导语：浅谈拓扑伽罗华理论

原创 顾险峰 老顾谈几何 和汪浩然探讨Arnold所创立的拓扑Galois理论，汪浩然比较认同Arnold的观点，Arnold认为应该用初等古典的观点讲解现代数学，而非用故弄玄虚的现代抽象观点讲解初等数学。这里，我们用Arnold的拓扑方法来解释抽象的Galois理论。

可解群

求解多项式方程是代数学的基本问题之一。Abel证明五次方程无“代数”解（即解无法由方程的系数通过算术运算与求根运算表达），Galois完整地解决了多项式的根求解问题：他给出了多项式根式可解的充分必要条件。与多项式可解性密切相关的群是对称群。

所谓群是一个集合和一个乘法算子, 满足条件

封闭性：单位元：, , 都有可逆性：, , 使得结合律：, 都有

例如考察数列的所有排列，以排列的复合为乘法，构成所谓的对称群。对称群由所谓的对换生成，所有由偶数个对换生成的排列构成所谓的交错群。

我们注意到，群的条件中不包含可交换性，即可能。如果乘法可交换，那么群被称为是Abel群，否则是非Abel群。衡量一个群到Abel群的距离，要用到换位子群的概念。设为群，称由集合

生成的子群为的换位子群（Communtator Group），记作. 如果是Abel群，则换位子群为. 我们递归构造如下：

如果存在一个整数，使得，那么我们说群是一个可解群。（这里可解群的定义和传统定义不同，但是彼此等价）。例如，令，直接计算中元素的个数，

群GG&39;&39;&39;S221S3631S4241241S5120606060这意味着，是可解群，但不是可解群，其交错群的换位子群等于自身，，因此不是可解群。根式解存在性给定一个多项式我们将复平面并上一个无穷远点,通过球极投影映到单位球面上. 再将： 看成是从球面到自身全纯映射，. 当时， ，我们在平面上围绕无穷远点画一个小圆，由最高项，是平面上围绕点的转了圈的圆。这意味着是将源球面包裹了目标球面，一共包裹层。因此对于目标球面上的任意一点，在源球面上存在个原像，因此即次代数方程有个复数根。这时，存在因式分解，由此，我们得到韦达定理

即多项式的系数是其根的基本对称多项式决定。我们重新排列这些根，， ，由韦达定理不变，即多项式方程不变。Galois理论基本上是说如果次代数方程有代数根式解，那么是可解群。对于和,是可解群，因此存在求根公式；对于，不是可解群，因此不存在求根公式。传统抽象代数的证明需要较多基础知识，包括域扩张理论，下面Arnold的拓扑证明非常初等且简洁。

根的排列

我们考察多项式

记所有系数构成的复向量为，。令所有的根依随时间变动，其轨迹为，. 这时左侧多项式也依随时间而变化，

图1. 设计根路径。

如图1所示，对于任意的排列，我们可以设计路径，，满足

由韦达定理，我们有，这意味着系数向量构成一个圈，记成.

引理1. 假如代数方程存在求根公式， ，系数沿着跑了一圈，那么自然地我们有下面的等式这里是的简写，即求根公式的起止点函数值所得到的排列，等于方程的根的排列。

例如，我们考察一元二次方程

令，，则, 。令为对换，

构造为上半圆弧，从到达；令为下半圆弧，从到达,

由此我们得到系数环路,

我们知道，一元二次方程的求根公式：

这里

当从变到时，从变到；从变到. 这意味着求根公式的起始和终止值得到了根的排列，等于初始设计时用到的,

一般的求根公式由有理函数和开根号运算复合而成，例如：这里是的有理函数。核心想法：我们希望验证任何形式的都不是的求根公式，如果我们能够找到一条系数空间中的环路，使得引理1中的等式不成立即可。我们下面构造如此的环路，使得，但是右侧根的排列不是恒同变换，如此产生了矛盾。这可以用换位子的技术实现。

Monodromy

上面的讨论中，有一点非常令人迷惑：我们令系数跑了一个环路回到起点，，但是求根公式确不等于. 这涉及到monodromy的概念。我们用拓扑的观点来解释。

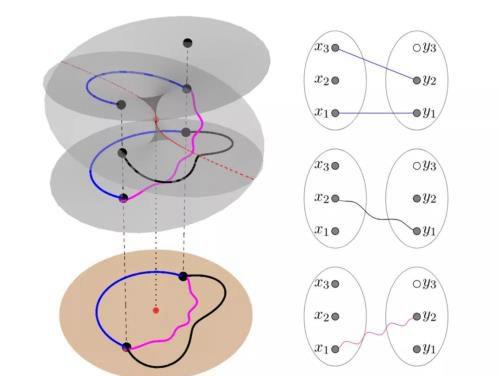
图2. 道路的提升和Monodromy.

前面我们谈到，多项式 可以视为从-球面到-球面的保角变换，把源球面包裹在目标球面上，包裹了层。如图2所示，映射的导数为

的零点为映射的分支点，其他的正常点处，映射局部可逆。整体上映射是-重分支覆盖，我们将-球面看成-球面的覆盖空间。的原像即为的根，假设它们都是正常点. 我们在-球面上画一条环路，。我们选取的一个邻域，在此邻域内恒不为，因此映射可逆。我们将曲线通过逆映射映回到-球面，得到一段曲线，记为, 我们说是在中的提升。然后，我们再在-球面上选取邻域，非空，同时在上可逆，那么可以将提升到中。如此重复，一直到把提升到覆盖空间（-球面）中的一条道路。由，, ,我们得到。同理，我们从开始提升到覆盖空间中，得到，那么这些提升道路的起止点给出了的一个排列：

那么我们将成为是的monodromy.

在我们的情形，环路的变量是系数而非，但是思想类似。

换位子技巧

现在我们来考察核心技巧，换位子。给定两个排列，对应的系数环路为和. 排列的换位子和环路的换位子分别为

这里是一个排列，依然是系数空间中一条环路，先沿着走一圈回到原点，再沿着走一圈，然后逆向沿着走一圈，最后逆向沿着走一圈回到原点。

我们先证明一个简单的命题：

命题1：三次方程代数求根公式不可能具有形式：

下面的观察是关键的：

引理2：给定次多项式，对于任意，任意的，，是如上构造的环路，沿着环路变动，那么

这里是有理函数。

引理2的证明：这个证明是初等的，，因此它们的幅角相差的整数倍。由定义

幅角变化量相抵相消，总幅角变化量为引理得证.

命题1的证明：由上面的表格，我们有有个元素，因此存在排列，使得。同上构造系数空间的环路，，考察命题1中的求根公式的起止值，由引理2它们相等，，但是引理1中的右侧，三个根的排列为，因此引理1中的等式不成立，矛盾。由此命题1正确。

我们再来证明类似的命题：

命题2：四次方程求根公式不可能具有形式：

证明：由上面的表格，我们有有个元素，因此存在排列，使得

同上构造系数空间的环路，，，. 用一次引理2，我们有：当沿着跑一圈，或者沿着跑一圈， 都得到

再用一次引理2，当沿着跑一圈, 我们有

但是引理1中的右侧，四个根的排列为，因此引理1中的等式不成立，矛盾。由此命题2正确。

我们现在可以证明经典Abel-Galois定理：

定理：五次代数方程没有代数求根公式（只包含算数运算和根式运算）。

证明：反证法，假设存在求根公式，一共嵌套了重根号. 因为有个元素，肯定存在一个排列，。

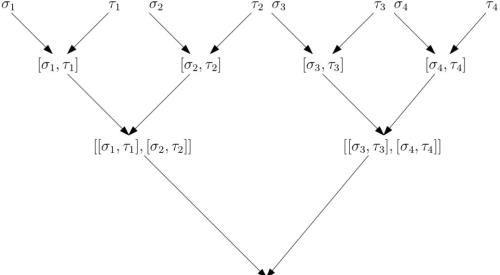
图3. 多重换位子

如图3所示，存在个排列，，在重换位运算下等于. 如上构造系数空间的环路和，同样运用重换位运算，得到。次运用引理2，我们得到结论：如果沿着跑一圈，那么求根公式，

但是引理1中等式的右侧根的排列为，引理1中的等式不成立，矛盾。因此假设错误，不存在求根公式带有重的嵌套根号。由的任意性，我们知道五次方程不存在只包含算数运算和根号运算的求根公式。

高次方程求根公式存在性证明与此类似，不可解，对于任意的，，我们可以找到， ，从而构造. 对于任意具有重嵌套根号和算数运算的表达式，令沿着跑一圈，，但是根的排列为, 矛盾。

小结

这里我们用拓扑方法证明了次多项式代数方程求根公式存在性的Abel-Galois定理，其核心思想是拓扑中覆盖空间的monodromy的想法：如果阶对称群不可解，对于任意包含重嵌套根号和代数运算的公式，我们能够找到特殊系数环路，使得系数沿着跑一圈，方程的根重新排列，但是的起始值不变，因此不是求根公式。这种方法比抽象代数方法更加直观简洁，实质上，这种想法比Galois的结论更强，这种方法可以推广到更加复杂的表达式，可以包含算数运算、根号运算、微分、积分运算，甚至更加复杂的运算。同时，对于算法设计而言，这种方法直接指向了强大的同伦算法，在计算代数领域举足轻重。我们从中也体会出拓扑和代数，相互纠缠，和谐统一！傍晚时分，暴雪停歇，邻居们拉着雪橇上街遛娃，远方彩霞满天...—— 虎年将近，谨以此文纪念Abel和Galois.

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小舻创作整理编辑！