树里面含有什么(树含有的元素)

导语：知道含树为什么那么难吗？

给高一的孩子们讲函数的基本性质，课间孩子们递给我一张图，问：老师，您看这是神马呀？

我愕然，虽然不知道是什么，表面还得故作镇定，左边好像是一只小鸡，右边好像是一节莲藕，这到底是什么呢?

学生们早忍不了了，异口同声地说：这就是您刚才讲的奇函数和偶函数呀!

我去，含树啊，是这么个含法。。。

好吧，00后的孩子们有创意啊.不过，各种树都被你们玩坏了，你们考虑过树的感受吗......

来来来，我们一起看看学过的这些......含树.

第一类，按函数的性质分类，分为奇函数和偶函数，增函数和减函数.

奇函数

若对于定义域内的任一x，都有f(-x)=-f(x)，则函数f(x)为奇函数.比如函数y=x，y=sinx，y=x^3等均为奇函数.

奇函数的图象关于原点对称.

偶函数

若对于定义域内的任一x，都有f(-x)=f(x)，则函数f(x)为偶函数.比如函数y=IxI，y=cosx，y=x^2等均为偶函数.

偶函数的图象关于y轴对称.

增函数

注意看，树是不是越来越大、越来越多呢？

如果对于函数f(x)定义域的某个区间D上的任意两个自变量的值x1，x2，当x1<x2时，都有f(x1)<f(x2)，那么就说函数f(x)在区间D上是增函数；反之为减函数.

当我们描述函数的单调性时，必须指明在哪个区间上.比如函数y=x^2，在负区间上是减函数，在正区间上是增函数，不能笼统地下结论.

增函数在图象上表现为上升，减函数在图象上表现为下降.

第二类，从具体的函数类型出发，分为指数函数、对数函数、幂函数、三角函数等.

先看第一个...含树.

这两个函数联系非常紧密，互为反函数，即你的定义域为我的值域，你的值域为我的定义域.

直接上图，帮大家回顾二者的性质.

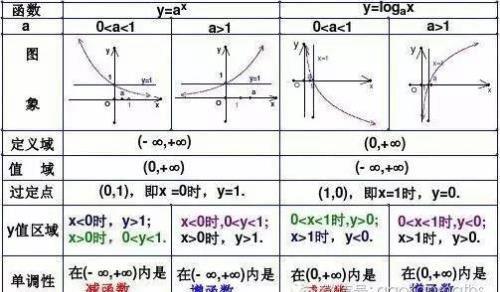
再看第二个...含树.

幂函数的形式为y=x^a（a取任意实数），请注意，幂函数的形式与指数函数的形式是不同的.随着a的变化，幂函数可以有很多个.在高中阶段，我们重点掌握5个幂函数，即a=1,2,3,-1,0.5的情况.

直接上图，我们一起来温习它们的图象和性质.

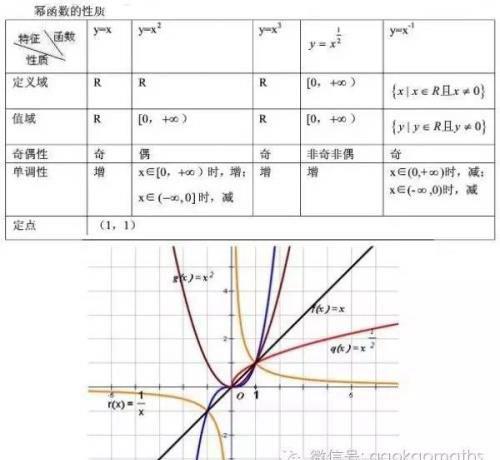
继续看第三个...含树.

我们学到的三角函数主要有三个：正弦函数y=sinx，余弦函数y=cosx，正切函数y=tanx.

在屏幕前的你，找一张白纸，画一画这三个函数的图象，你能画对吗？

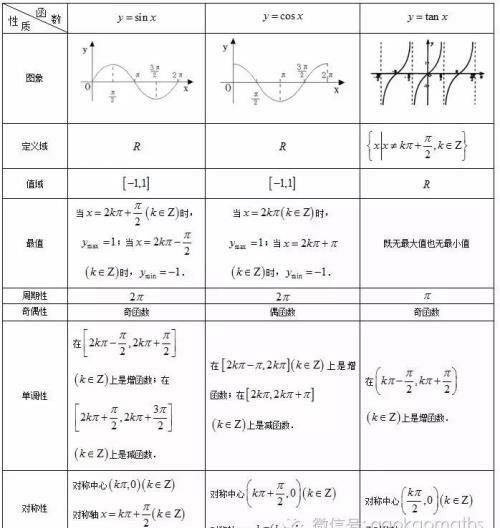
最后我们再来看一个...含树.

这个函数在教材里没有专门讲到，只在课后习题里出现过，但是在童鞋们的考试中，出现的频率非常高.

一般我们把函数f(x)=ax+b/x(a>0,b>0)称为对勾函数，它是一个奇函数，因为图象形似老师判卷时的对勾而得名，也有人称它为“耐克函数”（形似耐克图标），它的图象如下图所示.

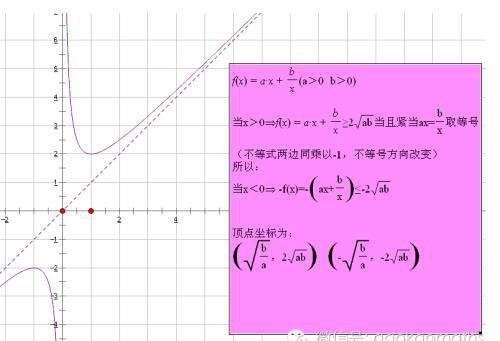
第三类，抽象函数.

知道函数为什么这么难了吗？

既要嘴里含树，又要挥鞭抽象，太难为宝宝了不是？

那究竟什么是抽象函数呢？

我们把不给出具体解析式，只给出函数的特殊条件或特征的函数即抽象函数.比如，已知函数f(x)满足f(x+y)=f(x)+f(y)对于任意x,y均成立，请你研究函数f(x)的奇偶性.

关于这类函数的处理方法，我写过高一：抽象函数的处理方法，有兴趣的朋友们可以参考.

最后的最后，让我们来欣赏孩子们的佳作吧.

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小琪创作整理编辑！