导语：如何证明相邻自然数平方数区间必有素数存在？

我们将在本文中尝试证明如下数学规律：

除了1以外，任意相邻自然数平方数区间必有2个以上的素数存在。

我们从偶数在自然数中所占的比例为1/2，但偶数与自然数却是一样多的这个奇怪的数学现象谈起。

根据集合论，偶数与自然数一样多；然而，在直觉上，偶数在自然数中的比例应当是1/2；两者有矛盾吗？

偶数在自然数中的比例是多少？我们会不假思索的说是1/2，原因很简单：自然数中要么是奇数，要么是偶数。

然而有另外一个问题存在：自然数中，偶数与自然数谁多呢？说偶数少于自然数却又是错的。因为偶数是可以由自然数来计数的。我们可以把偶数的集合表达为{2n | n为任意自然数 }，而这意味着这两者可以建立一一对应的关系。从这个道理上来讲，偶数、奇数与自然数又应该是一样多的。

怎么解决这个问题上的表面冲突呢？其实很简单：给定任意大小的自然数N，我们可以确定如果n是一个偶数，并且n≤N，那么这样的自然数n的数量在所有不大于N的自然数中的比例是1/2或逼近于1/2。当N是偶数时，比例为固定的1/2；当N是奇数时，随着N值越大，比例始终略大但也越接近于1/2，也就是说当N作为奇数趋向于无穷大时，这个比例的极限是1/2。为什么要讲得这么复杂呢？因为其实我们直觉上认为偶数占自然数的比例是1/2的观念的真正含义其实是如此。而这种理解与偶数和自然数一样多的观念是并行不悖没有冲突的。

所以，我们不就可以直接说偶数在自然数中的比例是1/2以简化表达，虽然这其实不是指那种通常的比例看法：一个有限数量与另一个有限数量的比较。

同样的道理，我们说3k+1 (k为非负整数）(注：接下来本文中涉及到的k都为非负整数，不再另行注释）形式的自然数在全体自然数中的比例是1/3。而6k+1形式的自然数在全体自然数中的比例是1/6。

一个问题：不能为2、3、5、7整除的自然数在全体自然数中的比例是多少？

此时，我要问一个问题：

不能被2、3、5、7整除的自然数，在全体自然数中的比例是多少？

我们不妨把不能被2、3、5、7整除的自然数简记为M(4)数，这里的4指的是自然数中的这前4个素数。

如何计算M(4)数在全体自然数中的比例呢？

我的答案是：(1-1/2)(1-1/3)(1-1/5)(1-1/7)=8/35。

解决思路简述如下：奇数都不能为2整除，其所占比例为1/2；奇数中能为3整除的数占奇数的1/3，不能为3整除的数占奇数的2/3；于是既不能为2又不能为3整除的数，占全体自然数的比例是(1-1/2)(1-1/3)=1/3。事实上就是如下两种形式：6k+1与6k+5。我们知道，所有自然数可以平均分为6类：6k+1，6k+2，6k+3，6k+4，6k+5，6k。

所以，同理，我们很快就可以得出了上述答案。

我们不妨检验一下。怎么检验？我们以2×3×5×7＝210为模，不妨将自然数平均分成210类：{1+210k}，{2+210k}，{3+210k}，……，{206+210k}，{207+210k}，{208+210k}，{209+210k}，{210k}。

我们易于检验其中有48类是M(4)数，也即不能为2、3、5、7整除的自然数，事实上这些数的分布规律是以210为周期的，而48/210＝8/35。其中对应的48个类是：{1+210k}，{11+210k}，{13+210k}，{17+210k}，{19+210k}，{23+210k}，{29+210k}，{31+210k}，{37+210k}，{41+210k}，{43+210k}，{47+210k}，{53+210k}，{59+210k}，{61+210k}，{67+210k}，{71+210k}，{73+210k}，{79+210k}，{83+210k}，{89+210k}，{97+210k}，{101+210k}，{103+210k}，{107+210k}，{109+210k}，{113+210k}，{121+210k}，{127+210k}，{131+210k}，{133+210k}，{137+210k}，{139+210k}，{149+210k}，{151+210k}，{157+210k}，{163+210k}，{167+210k}，{169+210k}，{173+210k}，{179+210k}，{181+210k}，{187+210k}，{191+210k}，{193+210k}，{197+210k}，{199+210k}，{209+210k}。

对于任意一个自然数N，其范围内的M(4)数的比例，当N是210的整倍数时，其比例正好为8/35。若N不是210的整倍数，其比例会略高于8/35，随着N的值越大，总体会越趋近于8/35；但中间会有起伏，以210为一周期。如图所示：

这只是一个示意图。实际情形不是这种比较波动比较少的曲线，而是微小起伏比较多的，但最低点始终是8/35。也就是说，在全体自然数中，也即N趋向无穷大时，这个比例极限是8/35。

问题讨论完毕。

M(n)数在全体自然数中的比例

记P(n)为自然数中的第n个素数，譬如P(11)=31，因为31是自然数中的第11个素数。

然后我们定义M(n)数类。

定义一

我们定义M(n)为这样一种自然数类：这类自然数不能为任意P(i) (1≤ i ≤n) 所整除。

我们在上一节里已经讨论过M(4)数了。

由前述类似关于M(4)在自然数中的比例讨论，我们不难知晓如果自然数 D(n)=∏P(i) (i从1至n)，也即 D(n)是所有不大于P(n)的连乘积时，M(n)数在自然数 D(n)范围内的比例等价于其在全体自然数中的比例。

这意味着自然数 D(n)范围内的M(n)数的数量此时的值等于它的欧拉函数值。欧拉函数为：

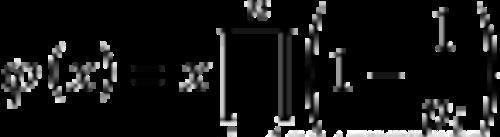
根据欧拉函数的规定，上式中的p_i (打不出下标，这里用_i表示下标）是x的所有素因数，具体到本例中，此时x= D(n)而p_i为P(i) (1≤ i ≤n)。从而M(n)在 D(n)中的比例为：

λ(n)=φ(D(n))/D(n)=∏(1-1/P(i)) (i从1至n)，λ(n)也是M(n）在全体自然数中的比例。

而对于任意足够大的并且非D(n)的整数倍的自然数N范围内，M(n）在N中的比例将会略大于λ(n)，也就是说N范围内的M(n)数的数量将会不少于[N×λ(n)](中括号表取整)。

如果自然数P(n)²＜N＜P(n+1)²，此时我们可以断言N范围内至少有素数:X(N)≥n+[Nλ(n)]－1。理由是：N范围内至少有[Nλ(n)]个M(n)数，而当m∈M(n)并且1＜m＜P(n+1)²时m必是素数，这意味着N范围内至少有[Nλ(n)]－1个数既是M(n)数又是素数（注意：1是M(n)数但不是素数）；从而，N范围内至少有n+[Nλ(n)]－1个素数（再加上n个P(i)素数）。

举个例子：

令n=4，随意假设N=72，X(N)≥n+[λN]－1＝4+[8/35·72]－1＝19。区间[1，72]范围内的素数多于19个，而有2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71等20个。

任意连续N个数中的M(n)数的比例

假设自然数区间[x，y]有连续N个自然数，并且N＞P(n)，那么这N个自然数中有多少M(n)数？

我们是否可以直接断定其至少有M(n)数[Nλ(n)]个？

我们不妨依然根据“筛法”来思考：

首先，还是还是得先筛去所有偶数；

然后，再筛去剩余的奇数中的3倍数；

……

也就是说：整个筛法的进程没有任何区别，差别只在于：与从自然数1开始筛起相比，x有可能被筛有可能被筛，起始顺序略有差别而已。但不管怎么变化，其包含有的M(n)数的比例不会少于λ(n)。

因此有：

定理一

对于任意连续N个自然数，如果N＞P(n)，至少有[Nλ(n)]个M(n)数。

相邻自然数平方数区间必有素数的证明

如果m是任意一个自然数，那么相邻自然数平方数(m²，(m+1)²)区间是否必然有素数呢？这个问题目前在数学上还依然是属于有待证明的。我们在这里将尝试利用前述的思路来探究这个问题。

存在如下三种情况：

P(n)＜m＜m+1＜P(n+1)，于是有：P(n)²＜m²＜(m+1)²＜P(n+1)².

P(n)≤m＜m+1＜P(n+1)，于是有：P(n)²≤m²＜(m+1)²＜P(n+1)²

P(n)＜m＜m+1≤P(n+1)，于是有：P(n)²＜m²＜(m+1)²≤P(n+1)²

不管是哪种情况，我们都只考虑[m²＋1，(m+1)²－1]这两种情况，也即总计连续2m个自然数。

根据上一节定理一，连续2m个自然数中至少有[2mλ(n)]个M(n)数。

由于：

λ(n)＝(1-1/2)(1-1/3)(1-1/5)……（1-1/P(n))

＝(1×2×4×6×10×……×(P(n)-1))/(2×3×5×7×……×P(n))

＞1/P(n)

从而：

[2mλ(n)]≥[2P(n)/P(n)]＝2 (注意：m≥P(n) )

这意味着当m≥P(n)时，任意连续2m个自然数中至少存在2个数必是M(n)数；也意味着连续m个自然数中至少存在1个数必是M(n)数。

也意味着(m²，(m+1)²)必有至少2个M(n)数，注意到(m+1)²≤P(n+1)²，于是可断定(m²，(m+1)²)区间的M(n)数必然是素数。

上述结论意味着如下定理二以及推论一：

定理二

除了1以外，任意相邻自然数平方数区间必有2个以上的素数。

推论一

任意相邻自然数平方数区间必有素数存在。

另：

“连续m个自然数中至少存在1个M(n)数”可以推出一个数论中的已知定理：

任意一个自然数的2倍数内必有素数存在。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小森创作整理编辑！