> 动物
三角形证明题及答案初二数学(初二下册数学三角形的证明)
导语:初二数学,一道典型的三角形证明问题,涵盖多种知识点
如图1,在△ABC中,AB=AC,D、E是BC边上的点,连接AD、AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′
(1)求证:△ABD≌△ACD′;(2)如图2,若∠BAC=120°,
①求∠DAE的度数
②当△CD′E是正三角形时,BD,DE,CE之间满足怎样的数量关系;

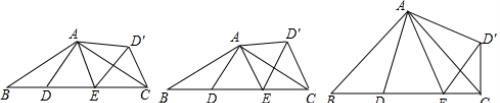
解析:
(1)△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E
可知:AD=AD′
∵BD=CD′,AB=AC
∴△ABD≌△ACD′
(2)解
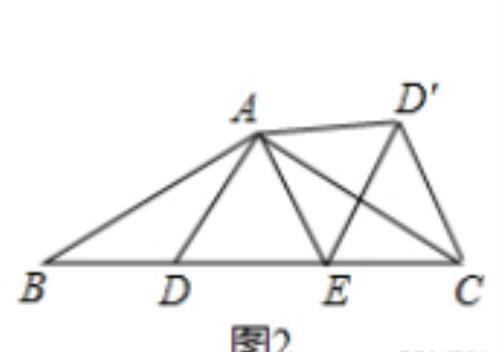
∵△ABD≌△ACD′
∴∠BAD=∠CAD′,
∴∠BAD+∠DAC=∠DAC+∠CAD′
即:∠BAC=∠DAD′
∵∠BAC=120°
∴∠DAD′=120°
∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴∠DAE =∠D′AE=∠DAD′÷2=60°
②∵△CD′E是正三角形
∴D′E=EC=CD′
∵D′E=DE,BD=CD′
∴DE=EC=BD
(3)
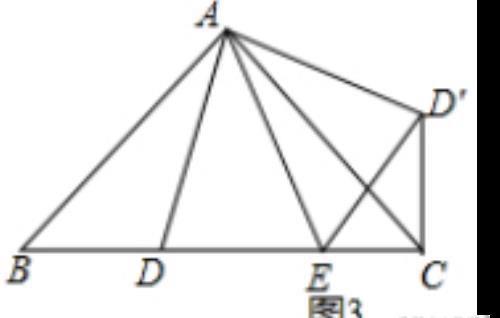
∵∠BAC=90°
∴∠B+∠ACB=90°
∵△ABD≌△ACD′
∴∠B=∠ACD′
∴∠ACD′+∠ACB=90°,即∠ECD′=90°

∵△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E
∴ DE=D′E,BD=CD′

谢谢您的支持和关注,欢迎交流
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小若创作整理编辑!