正十七边形问题的起源(正17边形长什么样子)

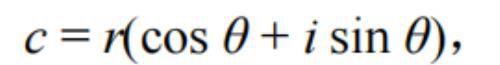
导语：正十七边形问题

把一个圆的周长分为十七等分

高斯在1801年出版的他的主要著作中解了这道著名的问题。该书涉及了二项方程x^n = 1，高斯证明了这个重要的定理：

一个正多边形当且仅当它的边数有2^mp1p2...pv的形式（这里p1，p2，...，pv均是不同的n ，才能用圆规和直尺作出其图形。

当m = 0，v = 1及p1 = 3与p1 = 5，分别得到正三角形与正五边形，这在古代已得到解答。高斯在他的研究结论中说：“在欧几里德时代已经知道把一个圆分成三等分或五等分。令人吃惊的是在以后两千年中没有新东西来充实这些发现，几何学家认为除了这些情况以及这些情况导出那些情况以外，使用圆规和直尺不能作正多边形。”

高斯之所以能在等分圆方面取得巨大的成就，仅仅是因为他将原来的纯几何题变成代数题。他是在以他的名字命名的高斯平面上复数表示中完成这一变换的。

在这个平面中，通常以具有坐标(a, b)的点表示任意复数c = a + bi；这个点本身称为“复数c”。另一种一般的方法是复数c的三角表示法

这里r表示数的大小（模数），即c与平面的原点O的距离，而数的角θ是由距离r和实数轴正向形成的角

以圆心O所画的单位圆R的点表示所谓的高斯数，也就是下面形式的数。

这里φ是数γ的角。

简写为

高斯数的基本性质可由一下关系式阐明

也就是说，两个高斯数的乘积亦是一个高斯数，其积的角是各因子角的和。

例如：

或者，完整地写为

这就A·棣美弗（Abraham Demoivre，1667 – 1754年）公式。

为了得到一个n个角的正多边形，开始顺次标出角ϕ=2π次，所得的点表示为：

那么

和

因此，n个角的正多边形的n个方程的根： 这样，根据高斯的解法，“画一个n个角的正多边形”的集合问题就变成“求方程z^n = 1的根”的问题。

由于该方程的n个根中的一个值为1，仅需要求出其余的n – 1个根。这些根满足方程 示为：

这就是所谓的圆分割方程。例如，就： 各个根为： n = 3来说，该方程为z^2 + z + 1 = 0。

由于复数ε和ε均具有实部-1/2，所以正三角形的角顶ε和ε是圆R通过点-1/2的虚轴平行线的交点。

定理的理论会扯得太远，所以这里近限于简述那些最正十七边形作图所必须的基本概念和要素。

首先注意2mN正多边形的作图相当于作正p边形、q边形、正r边形等等，这里N是奇素数p，q，r，...的乘积。若有了这些多边形，那么确定整数x，y，z，...，使

可以这样做是因为数

没有公因数。于是

结果，连接圆周长的，...便得到圆R的N分之一。

因此仅考虑分割方程

其中p是形如2^n + 1的素数。

高斯卓越想法包括将（1）各个根ε1，ε2，...，εp–1（这里εv = ε1^v = ε^v，ε = cos φ + i sin φ=2π/p组成所谓的周期。高斯周期是根的和 中每一相邻项是前一项的g次幂，p的原根，也就是这样一个整数，即gp–1是其中最小整数幂，该幂除以p得余数为1。换言之，g是这样一个下列形式表示： z = ε，z1 = ε−p。 ，其而总和末项的g次幂再次形成第一项（这样才称为周期）。指数g在这里是所谓的素数整数，使得（1）的根可以用

下一个周期是 z0 + z1 + z2 +...+ zp–2。 事实上

下面的周期只包含a=p-q/2项，并写成

在这个周期里，每一项是前项的G次幂，并且zrG = z0，这里G = g2同样是p的一个原根。

本文内容由快快网络小馨创作整理编辑！